摘要：
在计算机科学中，排序算法是一种常见的算法类型。而快速排序作为最常用的排序算法之一，在大数据集下具有优异的性能。然而，当待排序的数据集中存在重复元素时，传统的快速排序算法可能会导致时... 在计算机科学中，排序算法是一种常见的算法类型。而快速排序作为最常用的排序算法之一，在大数据集下具有优异的性能。然而，当待排序的数据集中存在重复元素时，传统的快速排序算法可能会导致时间复杂度升高。为了克服这个问题，分割数快速排序应运而生。本文将探讨分割数快速排序算法的原理、优势以及在实际应用中的可能应用领域。
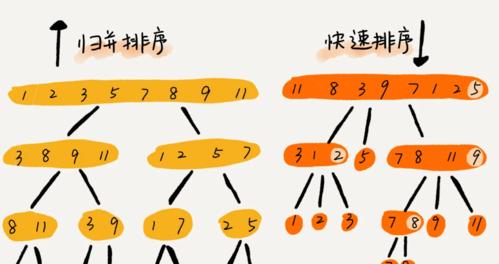
分割数快速排序：基本原理与思路
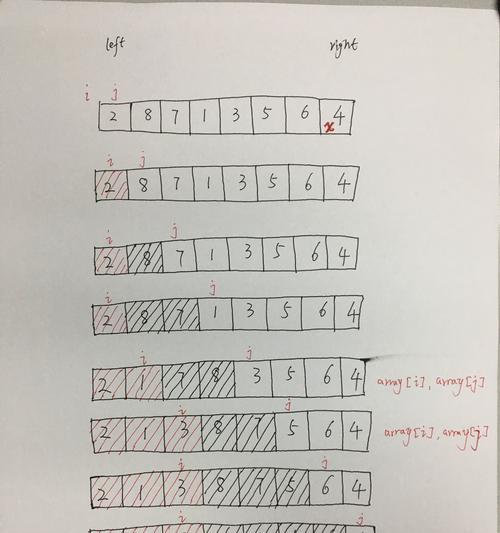
分割数快速排序的基本原理是将待排序数据集根据某个分割数（pivot）进行划分，使得左边的元素都小于等于分割数，右边的元素都大于等于分割数，然后对左右两部分递归地进行快速排序。通过选择合适的分割数和划分策略，可以有效提高排序效率。
优化快速排序：处理重复元素的挑战
传统的快速排序算法在处理存在重复元素的数据集时，可能会出现分割不均匀的问题，导致排序性能下降。分割数快速排序通过引入额外的操作，在划分过程中将等于分割数的元素均匀地分散到左右两部分，从而避免了分割不均匀的情况。
递归划分：迭代与递归的比较
分割数快速排序使用递归的方式进行划分，递归调用可以使算法更加简洁、易于理解。然而，递归调用也带来了一定的额外开销，可能导致栈溢出等问题。本节将对比迭代和递归的优缺点，并讨论在实际应用中如何选择合适的方式。
分割数的选择策略：影响排序性能的关键因素
分割数的选择对快速排序的性能有着重要影响。本节将介绍常见的分割数选择策略，如随机选择、三数取中法等，并分析它们的优劣势。同时，还将讨论针对不同数据集特征选择合适分割数策略的方法。
时间复杂度与空间复杂度分析
通过分析分割数快速排序算法的时间复杂度和空间复杂度，可以更好地了解其在不同规模数据集下的性能表现。本节将介绍分割数快速排序的最坏情况时间复杂度、平均情况时间复杂度，以及对比其他排序算法的优势。
应用领域一：大规模数据排序
分割数快速排序作为一种高效的排序算法，可以在大规模数据集下提供快速的排序能力。本节将探讨分割数快速排序在大数据场景下的应用价值，以及如何通过优化算法参数进一步提升排序效率。
应用领域二：模糊匹配搜索
在某些场景下，我们需要对包含模糊匹配搜索的数据集进行排序。分割数快速排序算法可以通过选择合适的分割数策略，使得匹配度高的元素尽量靠近分割数，从而加速模糊匹配搜索的效率。本节将介绍如何利用分割数快速排序算法进行模糊匹配排序。
应用领域三：图像处理
图像处理是一个复杂而庞大的领域，其中包含了各种各样的排序需求。分割数快速排序算法可以应用于图像处理中的各种排序任务，如像素排序、颜色排序等。本节将讨论在图像处理领域中如何利用分割数快速排序算法解决排序问题。
应用领域四：数据压缩
数据压缩是信息技术领域中的一项重要任务，而排序算法在数据压缩中也有广泛的应用。分割数快速排序算法可以通过对待压缩数据集进行排序，从而提高数据的连续性和压缩效率。本节将介绍在数据压缩领域中分割数快速排序的应用。
应用领域五：财务数据分析
财务数据分析需要对大量的财务指标进行排序和比较，以便提取有效的信息。分割数快速排序算法可以通过高效地对财务数据进行排序，为财务数据分析提供支持。本节将讨论分割数快速排序在财务数据分析中的应用案例。
优化策略一：并行计算
分割数快速排序算法可以通过并行计算技术，实现更高效的排序过程。本节将介绍如何利用并行计算技术优化分割数快速排序算法，并讨论并行计算对算法性能的影响。
优化策略二：内存管理
内存管理是影响排序算法性能的关键因素之一。本节将讨论如何通过合理的内存管理策略，减少分割数快速排序算法的额外开销，提高排序性能。
优化策略三：分布式计算
分布式计算是解决大规模数据处理问题的重要技术手段。本节将介绍如何利用分布式计算技术，将分割数快速排序算法扩展到大规模分布式系统中，实现更高效的排序处理。
应用案例一：股票数据分析
股票数据分析需要对大量的交易数据进行排序和比较，以便提取有效的交易信号。本节将以股票数据分析为例，探讨如何利用分割数快速排序算法进行股票数据的排序和分析。
分割数快速排序的价值与挑战
通过本文对分割数快速排序算法的探讨，我们可以看到其在各个领域中的广泛应用。然而，分割数快速排序算法也面临着一些挑战，如参数选择、递归开销等。我们需要在实际应用中根据具体问题选择合适的优化策略，以实现更好的排序性能。